Easily create cool random images in python with randimage

I was plan­ning to add pro­file pic­tures to my now defunct social-app for musi­cians Riff on That and I want­ed to offer a ran­dom­ly gen­er­at­ed pic­ture as a default option. I had a look around for exist­ing solu­tions in python and could­n’t find any­thing to my lik­ing, so I came up with randimage. This is a sim­ple pro­ce­dure that looks good to me, is sim­ple to under­stand and is mod­u­lar enough to exper­i­ment in the future with new vari­a­tions. You can find the code and instruc­tions on github - this post is meant as a more detailed expla­na­tion of how the pro­ce­dure works.

How randimage works

At the core the pro­ce­dure is com­posed of two sim­ple steps:

1. gen­er­ate a ran­dom region-fill­ing path
2. col­or the pix­els along the path using a col­ormap from matplotlib.

The idea is to lever­age the many beau­ti­ful col­ormaps avail­able in mat­plotlib to avoid rein­vent­ing the wheel — these offer a con­ve­nient way to con­tin­u­ous­ly map any num­ber between 0 and 1 to a col­or belong­ing to a spe­cif­ic curve in col­or-space. It is then enough to vec­tor­ize the image along some ran­dom path (step 1) and map point k in the path to k/N (where N is the length of the path), col­or­ing the cor­re­spond­ing pix­el with the val­ue of the cho­sen col­ormap for k/N.

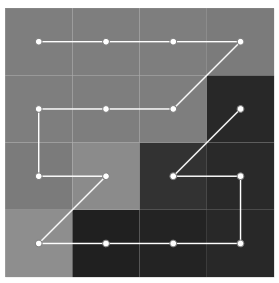
Finding a path with EPWT

I had sev­er­al ideas in mind on how to find an inter­est­ing path (some of which I men­tion in the last sec­tion of this post), but to my delight the first try — the EPWT [1] applied to a ran­dom­ly gen­er­at­ed mask — gave quite inter­est­ing results so I decid­ed to pub­lish it as-is and maybe down the line play with oth­er variants. 

EPWT stands for “Easy Path Wavelet Trans­form” and it was pro­posed in [1] by my PhD super­vi­sor Ger­lind Plon­ka. The pro­ce­dure is used for sparse image rep­re­sen­ta­tion (e.g. image com­pres­sion) and con­sists in apply­ing a 1‑dimensional wavelet trans­form to a vec­tor­ized ver­sion of the image obtained through a greedy path-find­ing pro­ce­dure, aimed at obtain­ing a suc­ces­sion of pix­el val­ues with min­i­mal vari­a­tion (which is a good thing for com­pres­sion). It is a cool idea and there are many details and pos­si­ble vari­ants (includ­ing my own Region Based vari­ant, the RBEPWT [2]).

More specif­i­cal­ly the EPWT greedy path-find­ing pro­ce­dure always picks as next point (among the avail­able neigh­bors) the one that gives the min­i­mum absolute val­ue dif­fer­ence in pix­el val­ues. Gen­er­al­ly speak­ing it will thus try to first fill in regions with sim­i­lar pix­el val­ues before mak­ing a jump and mov­ing on to much lighter or dark­er regions.

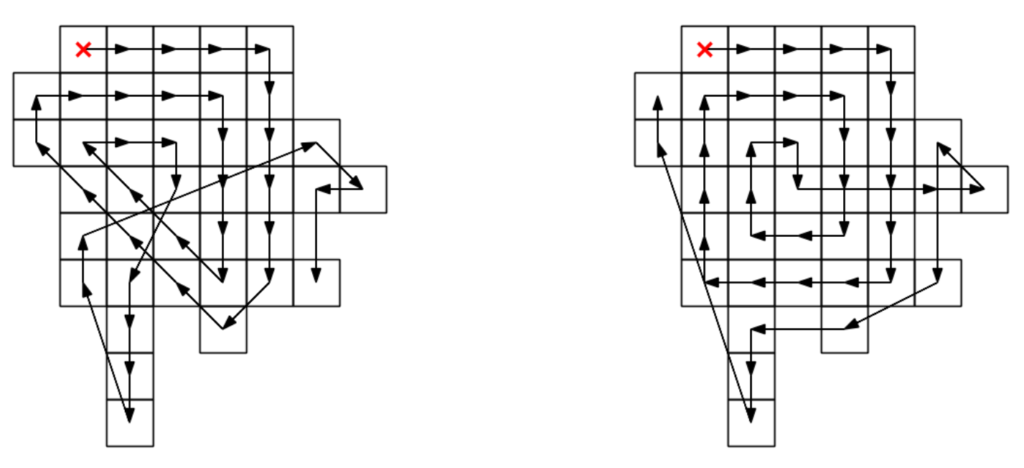
Mask -> EPWT -> color map -> profit

Sum­ma­riz­ing, the idea is then to:

• cre­ate a ran­dom gray-val­ued mask image with same dimen­sions as the final image
• apply the EPWT path-find­ing pro­ce­dure (start­ing from a ran­dom­ly cho­sen point)
• pick a ran­dom col­or map cmap
• map point k in the path to cmap(k/N)(wher N is the length of the path)
• … hope to get a cool result. 

Generating a mask

One way to gen­er­ate the mask is to sum var­i­ous Gauss­ian func­tions cen­tered ran­dom­ly in the image (in the code I do this by con­volv­ing a Gauss­ian fil­ter with an array that is zero every­where except for the cho­sen cen­ters, where it is one). This often results in a struc­tured EPWT path that approx­i­mate­ly fol­lows the lev­el curves of the mask; here you can see one such mask and the image obtained using the EPWT path and the Spec­tral colormap:

A variant: stochastic EPWT

I also imple­ment­ed a sto­chas­tic path find­ing pro­ce­dure in the ProbabilisticPath. Like the EPWT, at each step the pix­el val­ues of the avail­able neigh­bors of a point are con­sid­ered, how­ev­er now the next point is cho­sen ran­dom­ly among these using the pix­el val­ues as weights for the choice. In the fol­low­ing pic­ture you can see a mask (gen­er­at­ed with the GaussianBlobMask class), the EPWT path and the prob­a­bilis­tic one:

Since the white areas in the mask cor­re­spond to high­er prob­a­bil­i­ties, these act as sort of attrac­tors for the prob­a­bilis­tic path. 

What now?

The mod­u­lar­i­ty of the pro­ce­dure means we can try to sub­sti­tute var­i­ous parts of it to obtain new types of images. For exam­ple I thought of gen­er­at­ing a ran­dom image seg­men­ta­tion and then apply­ing the RBEPWT, which defines a path-find­ing pro­ce­dure that will fill a region based on its shape rather than its pix­el values:

You can read about the RBEPWT in [2] or in even more detail in Chap­ter 3 of my PhD dis­er­ta­tion [4].

Giv­en that the images with struc­ture seem to look cool­er and have more wow-effect, I would like exper­i­ment to with more rule-based pro­ce­dures to gen­er­ate paths tak­ing inspi­ra­tion for exam­ple from the flood fill algo­rithm or from cel­lu­lar automa­ton.

About me

I’m a Math PhD cur­rent­ly work­ing in Blockchain Tech­ni­cal Intel­li­gence. I also have skills in soft­ware and data engi­neer­ing, I love sports and music! Get in con­tact and let’s have a chat — I’m always curi­ous about meet­ing new people.

References

[1] Ger­lind Plon­ka. The easy path wavelet trans­form: A new adap­tive wavelet trans­form for sparse rep­re­sen­ta­tion of two-dimen­sion­al data. Mul­ti­scale Mod­el­ing & Sim­u­la­tion, 7(3):1474–1496, 2008.

[2] Budinich, R. (2017). A region-based easy-path wavelet trans­form for sparse image rep­re­sen­ta­tion. Inter­na­tion­al Jour­nal of Wavelets, Mul­tires­o­lu­tion and Infor­ma­tion Pro­cess­ing, 15(05), 1750045.

[3] Ma, J., Plon­ka, G., & Chau­ris, H. (2010). A new sparse rep­re­sen­ta­tion of seis­mic data using adap­tive easy-path wavelet trans­form. IEEE Geo­science and Remote Sens­ing Let­ters, 7(3), 540–544.

[4] Budinich, R. (2019). Adap­tive mul­ti­scale meth­ods for sparse image rep­re­sen­ta­tion and dic­tio­nary learn­ing (Doc­tor­al dis­ser­ta­tion, Nieder­säch­sis­che Staats-und Uni­ver­sitäts­bib­lio­thek Göt­tin­gen).